Stoichiometry Tutorials: Making a Standard Solution from Another Solution: Dilution
(from a complete OLI stoichiometry course)When you work in a laboratory, chances are you are starting off with a concentrated stock solution. Being able to create solutions of varying concentration from this is a useful skill. Solutions with known concentrations are often called "standard solutions." You can learn about the concept of dilution and how to use dilution to make a standard solution from a stockroom solution in the following video.
Dilution Movie Text
When we add water to a solution, we lower the concentration of the substances dissolved in that solution through a process called dilution. We can take advantage of dilution to make solutions of any desired concentration when we start with a more concentrated solution. Consider, for instance, a chemical stockroom that contains a solution of 1.00 M glucose. Let's say we want to make a solution that is 0.50 M in glucose; i.e., we want to cut the concentration in half. We can do this by mixing equal volumes of our 1.00 M glucose solution with distilled water. For example, if we mix 1.0 liter of 1.0 M glucose with 1.0 liter of distilled water, we double the volume to 2.0 liters and cut the concentration in half to 0.50 M.
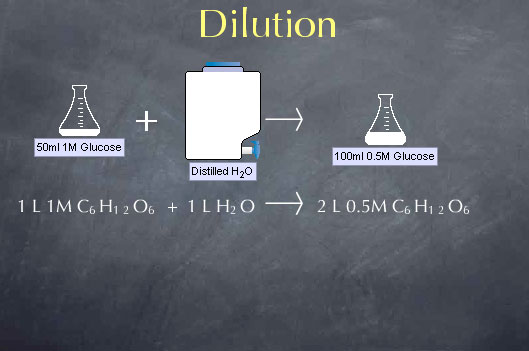
To understand the effects of dilution on concentration, we note that the amount of glucose is not altered by adding water to the solution. Adding water to the solution doesn't make or destroy glucose molecules. This means that the number of moles of glucose present before the dilution is equal to the number of moles of glucose present after the dilution.

Before the dilution we had 1.0 mole per liter * 1 liter, or 1.0 mole of glucose. After the dilution with have 0.5 moles per liter * 2 liters, or, again, 1.0 mole of glucose. This a particular instance of a more general expression for dilution, C1 V1 = C2 V2. C1 and V1 are the concentration and volume of the solution before the dilution. Their product C1 V1 is the number of moles of glucose present before the dilution. Similarly, C2 V2 is the number of moles of glucose present after the dilution. C1 V1 = C2 V2 captures the fact that dilution does not change the moles of glucose or other solute.

Say I want to make 100 mL of 0.29 M glucose, and my starting material is 1.0 M glucose. How do I go about this? I start with my expression C1 V1 = C2 V2. I then consider what I know about this situation. I know that my initial concentration, C1, is 1.0 M. I also know that my desired concentration after the dilution, C2 is 0.29 M. I know that I want to make 100 mL of solution, so my volume after the dilution, V2, is 100 mL. I can solve this for V1, my volume before the dilution, and get 29 mL. Note that I do not need to convert the volume from mL to liters. The units of molarity cancel, giving me V1 in units of mL.

So how would I perform this dilution in the laboratory? V1 is the volume of the solution before the dilution, so I begin by taking 29 mL of 1.0 M glucose. V2 is the volume after the dilution, meaning that after I add the water, the volume should be 100 mL. To get a final volume of 100 mL, I add 100-29 or 71 mL of water. Adding 71 mL of water will give me 100 mL of solution with a concentration of 0.29 M.
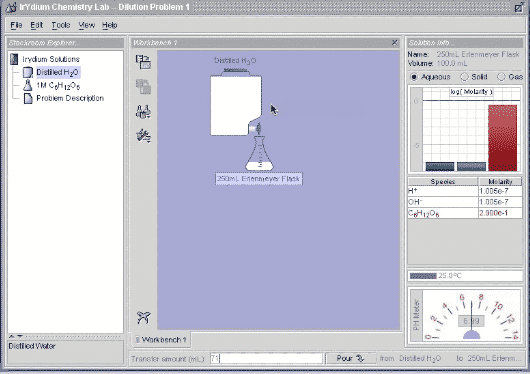
Let's go do this in the Virtual Lab. I take 29 mL of 1.0 M glucose and add 71 mL of distilled water, and you can see that I get 100 mL of 0.29 M glucose.